I animated so you could stare. 2025-07-15

Figure 1: The spherical harmonic of

r = Y_{2}^{1} (θ, ϕ)

. Color conveys the depth into page according to the key:

out of page

into page

The position of each

j th

Maomao of the

n = 1

shown uses the parameters:

θ (t) = \frac{2 π}{T} t + \frac{2 π (j - 1)}{n}, ϕ = \frac{16 π (j - 1)}{n}

in which

t

is the cyclic time of the animation ranging from

0

T = 8.0

seconds.

What Are They? 1

The spherical harmonics are a lot of things. I personally encountered them as part of a quantum mechanics course last spring.

The Chemist's Point of View 1.1

If you've ever seen the atomic orbitals, you may have noticed there's some pattern to their shape:

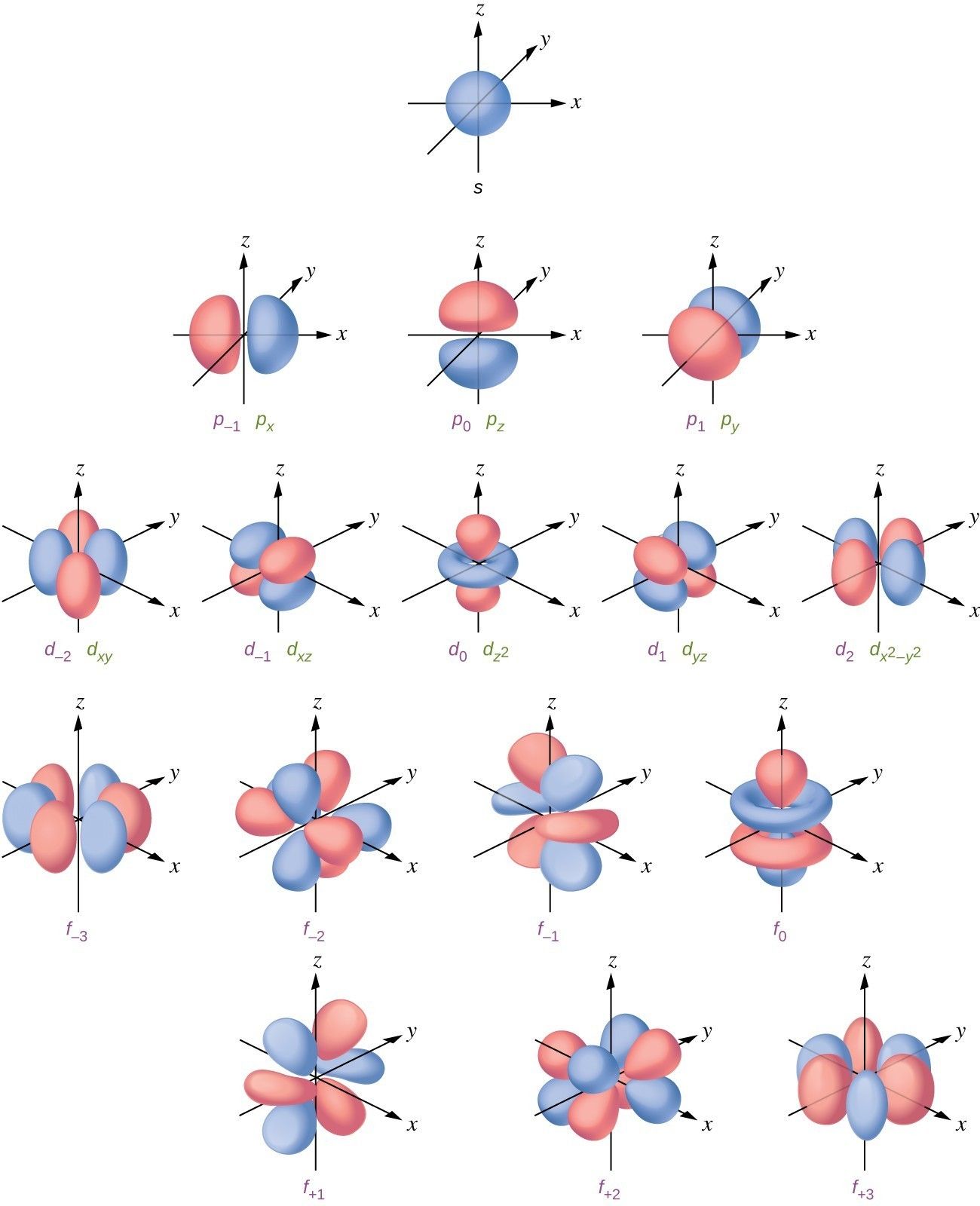
The atomic orbitals s,p,d,f — **Figure 2:** The atomic orbitals $s, p, d, f$ . The defining function yields positive values for points on blue surfaces, and negative values for points on red surfaces. The distance of a point on a surface from the origin denotes the magnitude of the function. Image courtesy of Learneo, Inc.

What defines these orbitals is the Hydrogen orbital wavefunction, which describes (among other qualities) the probability of the position of the electron

\begin{matrix} ψ_{n, l, m} (r, θ, ϕ) = \\ \sqrt{{(\frac{2}{n a_{0}})}^{3} \frac{(n - l - 1)!}{2 n (n + l)!}} \cdot e^{- r / 2 a_{0}} \cdot {(\frac{r}{a_{0}})}^{l} \cdot L_{n - l - 1}^{2 l + 1} (\frac{r}{a_{0}}) \cdot Y_{l}^{m} (θ, ϕ) \end{matrix}

Figure 3: The Hydrogen orbital wavefunction, which features the spherical harmonics:

Y_{l}^{m} (θ, ϕ)

Note that the spherical harmonic $Y_{l}^{m} (θ, ϕ)$ is the only term which depends on direction from the Hydrogen nucleus ( $θ$ or $ϕ$ ); all other terms are dependent only on constants and/or $r$ . Thus, the spherical harmonics are what give the Hydrogen orbitals their shape!

Hydrogen orbital (n,l,m)=(3,2,1) — **Figure 4:** The electron probability densities within the Hydrogen orbital $(n, l, m) = (3,2,1)$ a.k.a. $3 d_{xz}$ , which features the real spherical harmonic $Y_{2}^{1} (θ, ϕ)$ . Explore it in 3D at falstad.com.

The (Sloppy) Mathematician's Point of View 1.2

Another interpretation is listed on Wikipedia ⟩ Spherical harmonics, which may be more qualified than me on all its uses:

Since the spherical harmonics form a complete set of orthogonal functions and thus an orthonormal basis, every function defined on the surface of a sphere can be written as a sum of these spherical harmonics. This is similar to periodic functions defined on a circle that can be expressed as a sum of circular functions (sines and cosines) via Fourier series.

That is, in the same way one can redefine some periodic, univariate function by a possibly-infinite sum of sine waves...

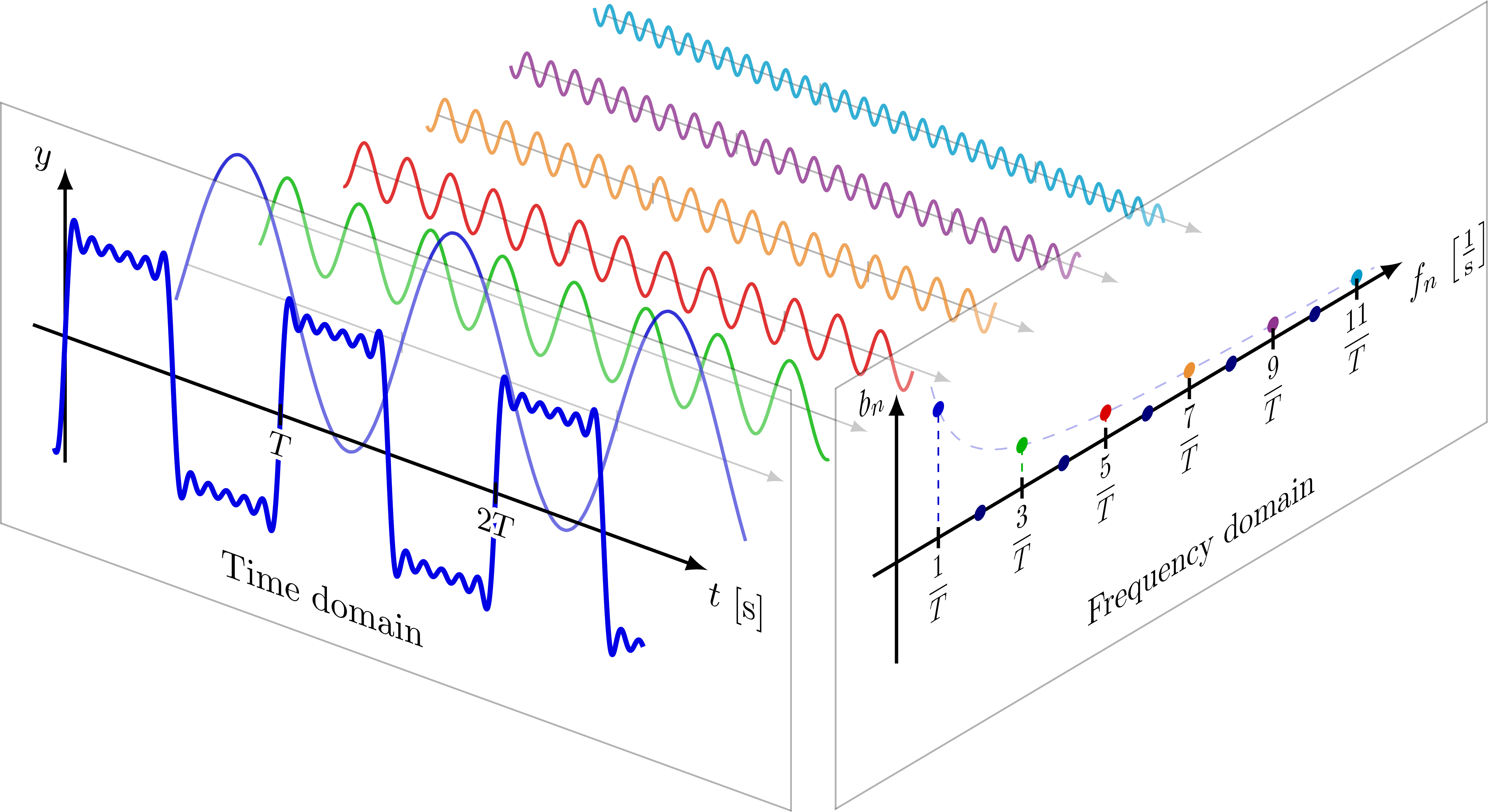
Fourier decomposition of a function into a sum of 6 sine waves — **Figure 5:** Fourier decomposition of a function (time domain) into its 6 constituent sine waves (frequency domain). Image courtesy of TikZ.net

...one could redefine some function which operates on the surface of a sphere (bivariate) using a possibly-infinite sum of spherical harmonics.

More Shapes and Maomaos 2

I find $Y_{2}^{1}$ to render nicely, hence why it is shown at the start of this article. However, I wrote the code to be parameterized over any $Y_{l}^{m}$ , and I wanted to have a grand display. Thus, there is now a real spherical harmonics page which allows exploring more shapes and shows even more Maomaos!

Final Remarks 3

I don't consider myself to have enough knowledge on the subject to describe them further in an abstract manner. Similarly, there are so many ways to define the functions and so much written about each definition that I don't see much value explaining the exact definitions this website used.

If you care to look into the spherical harmonics on your own, I found from my own research that it would've been helpful to know that there are three terms to describe them, which all point to the same concept with slight differences:

spherical harmonics
complex spherical harmonics: The functions which yield complex numbers. They may be constructed from the real spherical harmonics by
real spherical harmonics: The functions which yield real numbers. In terms of the complex spherical harmonics, only the real or imaginary component is taken depending on the sign of $m$ .

Note that each of the real and complex spherical harmonics can be defined independently or in terms of the other; they both refer to the same object, just produce values of a different type. See: Wikipedia ⟩ Spherical harmonics ⟩ Conventions ⟩ Real form.

This article has only discussed the real spherical harmonics, which I have more experience with and which also provide less information to visualize.